Wolfram|Alpha는 광범위한 연립방정식을 풀 수 있습니다. 1차 연립방정식과 비선형 방정식을 포함하는 연립방정식을 풀 수 있으며 정수 해와 다른 영역의 해를 구할 수도 있습니다. 또한 부등식과 보다 일반적인 제약 조건을 포함하는 시스템을 풀 수 있습니다.
온라인 연립방정식 솔버
Wolfram|Alpha로 방정식, 연립방정식 풀기
연립방정식과 제약 조건을 포함한 시스템의 해를 찾는 강력한 도구
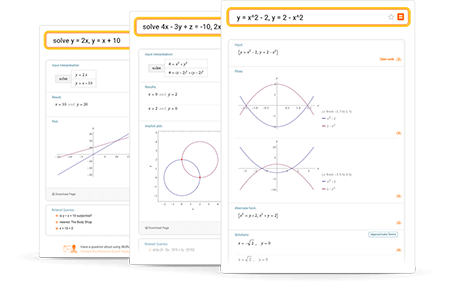
자세히 보기
쿼리 입력을 위한 팁
질문을 간단한 영어 평문을 사용하여 입력하세요. 애매한 질문을 피하려면 필요에 따라 괄호를 사용하세요. 다음은 연립방정식을 푸는 방법에 대해 질문하는 몇 가지 예시입니다.
즉시 학습 도구에 접근
단계별 해법 및 Wolfram Problem Generator로 즉각적 피드백과 도움을 얻으세요
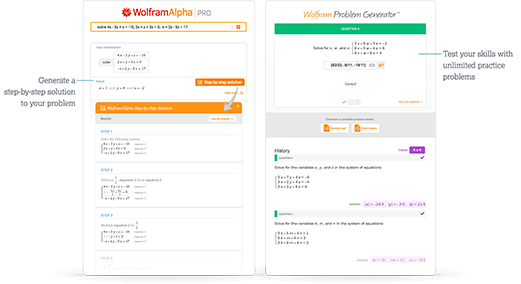
자세히 보기
연립방정식이란 무엇입니까?
연립방정식은 여러 변수가 있는 하나 이상의 방정식을 포함하는 집합입니다.
연립방정식의 해는 모든 방정식이 만족되는 변수의 대응 관계, 즉 모든 방정식이 교차하는 위치입니다. 연립방정식을 푼다는 것은 이러한 공통된 해 또는 교차점을 모두 찾는 것입니다.
연립 일차방정식은 일반적이고 적용 범위가 넓은 연립 방정식입니다. 두 개의 변수일 경우, 일차방정식은 2차원 공간에서 그려진 직선으로 생각할 수 있습니다. 만약 모든 직선이 공통의 한 점에서 교차한다면, 이 시스템은 일관성이 있다고 하며, 교차점에서 해를 가집니다. 그 외의 경우에는, 시스템은 불일치가 있다고 하며 해가 존재하지 않습니다. 두 개 이상의 변수를 포함하는 선형 방정식의 연립방정식도 유사하게 작동하며, 하나의 해를 가지거나, 해가 없거나, 무수히 많은 해가 있을 수 있습니다 (후자는 모든 구성된 방정식이 동일할 때 발생합니다).
비선형 함수를 포함하는 보다 일반적인 연립방정식도 있습니다. 이러한 연립방정식은 1개, 0개, 무한개 또는 임의의 수의 해를 가질 수 있는 보다 복잡한 해를 포함하고 있지만, 해가 관련된 모든 방정식을 만족하는 점이라는 점에서 선형 시스템과 유사하게 작동합니다. 더 나아가서 부등식을 포함하는 변수나 특정 변수가 정수인 등의 제약 조건을 가지는 보다 일반적인 연립방정식도 가능합니다.
연립방정식을 푸는 것은 매우 일반적이고 중요한 개념이며 수학, 공학 및 과학의 많은 분야에서 기초가 됩니다.