Wolfram|Alpha는 부정적분, 정적분, 이중적분, 삼중적분, 이상적분을 계산하기에 적합한 도구입니다. Wolfram|Alpha의 적분 계산기는 수학적 직관을 강화하는 데 도움이 되는 플롯, 대체 형식 및 기타 관련 정보도 표시합니다.
Online 적분 계산기
Wolfram|Alpha를 사용하여 적분 풀기
단순히 온라인 적분 계산기 그 이상
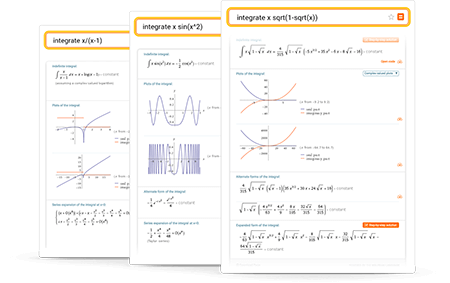
자세히 보기
쿼리 입력을 위한 팁
위의 수학 입력을 사용하거나 일반 영어 단어로 적분 계산기 쿼리를 입력하거나, 모호한 표현을 피하기 위해 필요한 부분에는 반드시 괄호를 붙입니다. 다음은 일반 영어로 적분을 요청하는 방법을 보여주는 몇 가지 쿼리의 예입니다.
즉시 학습 도구에 접근
적분 및 Wolfram Problem Generator에 대한 단계별 해법으로 즉각적 피드백과 도움을 얻으세요
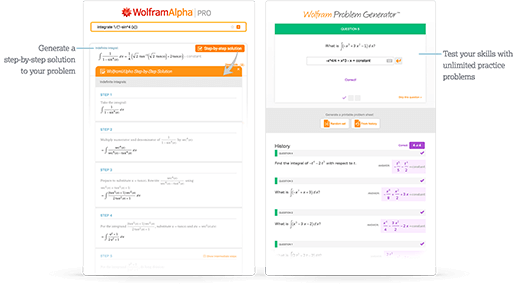
자세히 보기
적분이란 무엇인가요?
적분은 미적분의 중요한 도구로 부정적분을 구하거나 곡선 아래의 면적을 나타낼 수 있습니다.
f x의 부정적분은 f xdx으로 표시되고 이는 f x의 부정적분으로 정의됩니다. 즉, f xdx의 미분이 f x입니다. 상수의 도함수가 0이기 때문에 부정적분은 임의의 상수애 대해 정의됩니다. 예를 들어 −cosx + constant의 미분은 sinx임을 의미합니다. x = a에서 x = b까지의 f x의 정적분, 즉 baf xdx은 f x와 x 축 사이의 부호있는 면적을 x = a에서 x = b까지로 정의됩니다.
두 가지 유형의 적분 모두 미적분학의 기본 정리로 서로 연결됩니다. 이 정리는 f x가 a,b에서 적분 가능하고 Fx가 연속 부정적분이면 baf xdx = Fb - Fa가 됩니다. 즉 π0sinxdx = -cosπ - -cos0 = 2가 됩니다. 정적분의 근사값이 필요합니다. 이를 수행하는 방법은 곡선 아래에 얇은 직사각형을 두고 부호가 있는 영역을 더하는 방법이 잘 사용됩니다.
Wolfram|Alpha가 적분을 계산하는 방법
Wolfram|Alpha는 인간과 다른 방식으로 적분을 계산합니다. Wolfram|Alpha는 방대한 양의 수학적 그리고 계산적 연구 결과의 집합인 Mathematica의 Integrate 함수를 호출합니다. Integrate는 인간의 방식으로 적분을 계산하지 않고 대신 매우 정교한 수학을 포함하는 강력한 범용 알고리즘을 사용합니다. 이 알고리즘은 일반적으로 취하는 몇 가지 접근 방식이 있습니다. 첫 번째 방법은 적분의 일반 형식을 계산하고 이 형식을 미분하여 방정식을 풀어서 정의되지 않은 기호 매개 변수와 일치시키는 것입니다. 매우 간단한 적분 대상 함수의 경우에도 이 방법으로 생성된 방정식은 매우 복잡하며 Mathematica의 강력한 대수 계산 기능을 사용하여 해결해야 할 수도 있습니다. Mathematica가 적분을 계산하는 데 사용하는 또 다른 방법은 적분을 일반화된 초기하 함수로 변환하고 이러한 매우 일반적인 수학 함수에 대한 관계 모음을 사용하는 것입니다.
이러한 강력한 알고리즘을 통해 Wolfram|Alpha는 적분을 매우 신속하게 계산하고 다양한 특수 함수를 처리 할 수 있지만 인간이 적분을 수행하는 방법을 이해하는 것도 중요합니다. 결과적으로 Wolfram|Alpha는 단계를 따라 적분을 수행하는 알고리즘도 가지고 있습니다. 이 알고리즘은 인간이 적분을 계산하는 방법을 모방한 완전히 다른 적분 방법을 사용합니다. 여기에는 대입에 의한 치환 적분, 부분 분수에 의한 적분, 삼각함수 대입 및 부분 분수에 의한 적푼이 포함됩니다.