Wolfram|Alpha는 다항식 근을 찾고 방정식 시스템을 푸는 데 훌륭한 도구입니다. 또한 다항식을 인수분해하고, 다항식 해집합과 부등식을 그래프로 나타내며, 그 외에도 다양한 기능을 제공합니다.
온라인 방정식 솔버
Wolfram|Alpha로 선형, 이차, 다항 방정식 시스템을 풉니다
단순한 온라인 방정식 솔버 그 이상
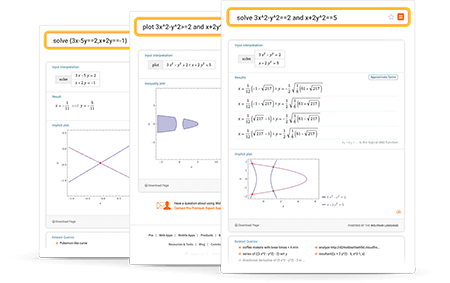
자세히 보기
검색어 입력을 위한 팁
쿼리를 간단한 영어로 입력하세요. 애매한 쿼리를 피하려면 필요한 경우 괄호를 사용하세요. 다음은 쿼리를 작성하는 방법을 보여주는 몇 가지 예시입니다.
학습 도구에 즉시 접근
단계별 해법과 Wolfram Problem Generator를 통해 즉시 피드백과 가이드를 받을 수 있습니다
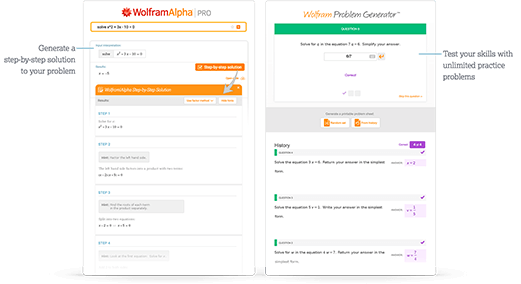
자세히 보기
방정식 풀기에 관하여
값 c는 pc=0일 때 다항식 px의 근이라고 합니다.
px에 나타나는 x의 가장 큰 지수를 p의 차수라고 합니다. px의 차수가 n이면, 중복을 고려할 때 n개의 근이 존재한다는 것은 잘 알려져 있습니다. 중복성의 의미를 이해하려면 예를 들어 x2 - 6x + 9=x-32=x-3x-3을 살펴봅니다. 이 다항식은 두 개의 근을 가지며, 두 근 모두 3과 같습니다.
보통 대수학의 두 번째 과정에서 유리수인 모든 근을 찾는 방법으로 "인수 정리"에 대해 배웁니다. 또한 필요한 경우 제곱근 (판별식에서 유도)을 사용하여 모든 이차 다항식의 근을 찾는 방법을 배웁니다. 3차 다항식과 4차 다항식의 근을 표현하기 위한 고급 공식이 있으며, 임의의 다항식의 근을 근사하는 수치적 방법도 여럿 존재합니다. 이는 복소 해석학의 방법과 정교한 수치 알고리즘을 사용하며, 실제로 이는 현재도 지속적인 연구 및 개발이 이루어지고 있는 분야입니다.
선형 방정식 시스템은 종종 가우스 소거법 또는 관련 방법을 사용하여 해결됩니다. 이는 일반적으로 중등 또는 대학 수학 교과 과정에서 접하게 됩니다. 비선형 방정식 시스템의 해를 찾기 위해서는 더 발전된 방법이 필요합니다. 부등식 시스템을 다룰 때도 비슷한 설명이 적용됩니다: 선형 대수학 과정에서 다루는 방법을 사용하여 선형 케이스를 처리할 수 있지만 고차 다항식 시스템은 일반적으로 더 정교한 계산 도구를 필요로합니다.
Wolfram|Alpha가 방정식을 계산하는 방법
방정식 풀이를 위해 Wolfram|Alpha는 Wolfram 언어의 Solve 및 Reduce 함수를 호출하며, 이 함수에는 기본적인 선형 및 이차 방정식에서부터 다변수 비선형 시스템에 이르기까지 다양한 종류의 대수 문제를 해결할 수 있는 광범위한 방법을 포함하고 있습니다. 경우에 따라 가우시안 소거법과 같은 선형 대수 방법이 사용되며 속도와 신뢰성을 높이기 위한 최적화가 적용됩니다. 다른 연산은 정수론, 추상 대수학 및 기타 고급 분야의 정리와 알고리즘에 의존하여 결과를 계산합니다. 이러한 방법은 Wolfram|Alpha를 사용하여 가능한 다양한 문제를 해결할 수 있도록 설계된 동시에 계산 시간을 최소화하는 데에도 중점을 둡니다.
이러한 방법은 직접적인 솔루션을 제공하는 데 유용하지만, 시스템이 인간이 동일한 문제를 어떻게 해결할지를 이해하는 것도 중요합니다. 따라서 Wolfram|Alpha는 인간이 쉽게 인식하고 따라가기 쉬운 고전적인 기법을 사용하여 대수 연산을 단계별로 보여주는 별도의 알고리즘을 가지고 있습니다. 여기에는 소거법, 치환, 이차 방정식 공식, 크래이머의 법칙 등이 포함됩니다.