Wolfram|Alpha는 1차, 2차, 3차 도함수, 임의의 점에서의 미분 계수 및 편도 함수를 푸는 데 적합한 계산기입니다. 도함수는 무엇이며 Wolfram|Alpha가 도함수를 계산하는 방법에 대해 알아보세요.
온라인 미분 계산기
Wolfram|Alpha를 사용하여 미분 풀기
단순한 온라인 미분 계산기 그 이상
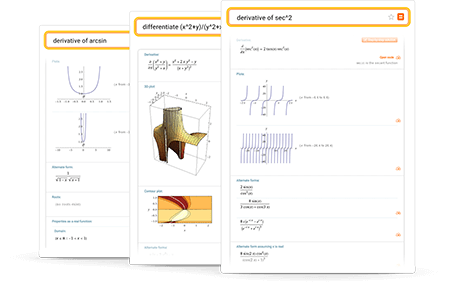
자세히 보기
쿼리 입력을 위한 팁
영어 평문으로 쿼리를 입력해주세요. 애매한 표현을 피하기 위해 필요한 부분에는 반드시 괄호를 넣어주세요. 아래는 미분에 대한 쿼리 예시입니다.
즉시 학습 도구에 접근
단계별 해법 및 Wolfram Problem Generator로 즉각적 피드백과 도움을 얻으세요
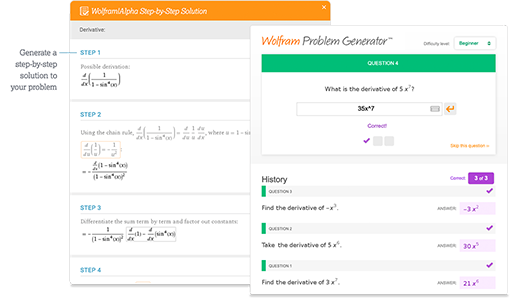
자세히 보기
미분이란 무엇인가요?
미분은 미적분에 중요한 도구로서 함수의 변수 중 하나에 대한 함수의 미세한 변화를 나타냅니다.
주어진 함수 f x가 있을 때, f를 x에 대해 미분한 것을 나타내는 방법은 여러 가지가 있습니다. 가장 일반적인 방법은 d fd x 와 f'x입니다. 미분을 n번 반복할 경우, dn fdxn 또는 fnx와 같은 표기가 사용됩니다. 이러한 미분을 고차 미분라고 합니다. 이차 미분의 경우 f''x이라는 표기가 자주 사용됩니다.
점 x = a에서, 도함수는 f'a = limh0f a + h - f hh 으로 정의됩니다. 이 극한은 항상 존재하는 것은 아니지만, 존재한다면 f x는 x = a에서 미분 가능하다고 말합니다. 기하학적으로 말하자면 f'a는 x = a에서 f x의 접선의 기울기입니다.
예를 들어 f x = x3라면, f'x = limh0h+x3-x3h = 3x2이고, 그 다음 f''x: f''x = limh03x+h2-3 x2h = 6x를 계산할 수 있습니다. 미분은 매우 강력한 도구로 다양한 응용이 가능합니다. 이를 통해 미분은 지역적/전역적 극값을 구하거나 변곡점을 찾고 최적화 문제를 해결하며 물체의 움직임을 설명할 수 있습니다.
Wolfram|Alpha가 미분을 계산하는 방법
Wolfram|Alpha는 표준 미적분학 교과서에서 찾을 수 있는 것보다 훨씬 더 큰 항등식 표를 사용하여 Mathematica의 D 함수를 호출합니다. 이 함수는 미분의 선형성, 곱셈 법칙, 거듭제곱 법칙, 연쇄 법칙 등 잘 알려진 규칙을 사용합니다. 또한, D 함수는 다양한 특수 함수의 미분을 계산하기 위해 잘 알려지지 않은 규칙도 사용합니다. 고차 미분의 경우, 일반적인 라이프니츠 곱셈 법칙과 같은 규칙을 사용하면 계산을 더 빠르게할 수 있습니다.